社会調査における量的調査では、その結果を統計的に処理して分析を行わなければなりません。
その手法について学びましょう。
量的データの分析ツール
度数分布表&ヒストグラム
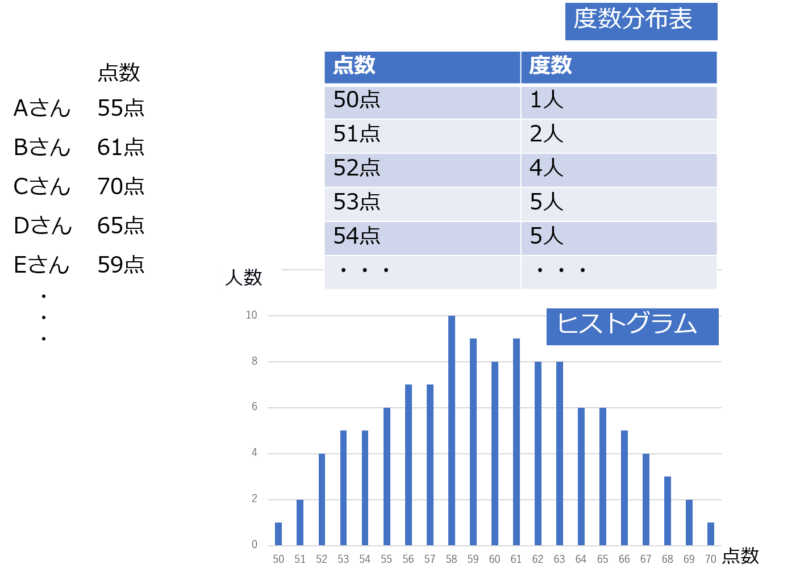
例えば、量的調査におけるアンケートで選択肢1を選んだ人が15人いたとすれば、15を度数といい、それらを表にしたものが度数分布表、グラフ化したものをヒストグラムといいます。
例えば、ある学校のあるクラスの生徒に対して、テストをした時の点数が下の表のようになったとします。このとき、ある点数の人が○人と以下のように表にしたものが度数分布表、グラフ化したものがヒストグラムです。
ある点数の人が何人というのが「度数」ですね。
代表値
度数分布表では平均値や中央値、最頻値といった「代表値」を求めることが出来ます。
平均値
平均値は、文字通り平均の値です。
テストの点数であれば、全員のテストの点数を足して、人数で割れば平均値が出ます。
中央値
中央値は、テストの点数を順番に並べてちょうど真ん中の点数のことです。
最頻値
最頻値というのは、最も多くの度数のある点数です。
グラフでいうと棒の一番長いところです。
例えば(1,1,2,4,100)の場合、平均値は21.6、中央値は2、最頻値は1です。
この例のようなハズレ値が含まれていると、平均値はハズレ値に影響されますが、中央値にはハズレ値に影響されないメリットがありますね。
正規分布
ヒストグラムでは、平均値を中心として山のような形状に近似できる場合があります。これを正規分布と呼び、テストの点数のバラツキなどはその典型です。
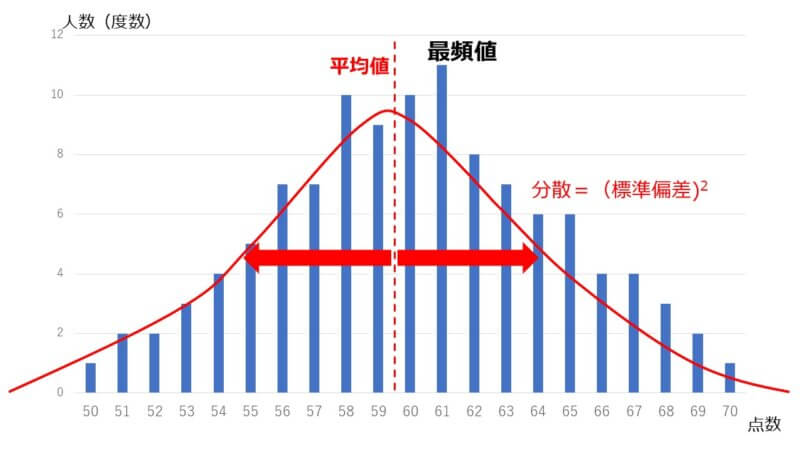
図では平均値が59.5点、その平均値を中心に左右にバラついています。
このバラツキの度合いを表すのが「分散」です。
すべての点数について平均値との差を二乗して平均を取った値です。
(二乗するのはマイナスの値をプラスにするためです。)
ただ、この値だと二乗しているので単位も二乗されて出てくるので、平方根をとって単位を元に戻した値が「標準偏差」です。
どちらも正規分布のバラツキを表す指標ですが、標準偏差=√分散 の関係にあることを覚えておいてください。つまり標準偏差を2乗すれば分散になります。
クロス集計表
度数分布表は1変数ですが、2変数以上の集計表をクロス集計表といいます。
先ほどのテストの点数について、例えばそれぞれの点数とか男女を書き込んでいくと変数が2つになります。
すると下のような表が出来ます。
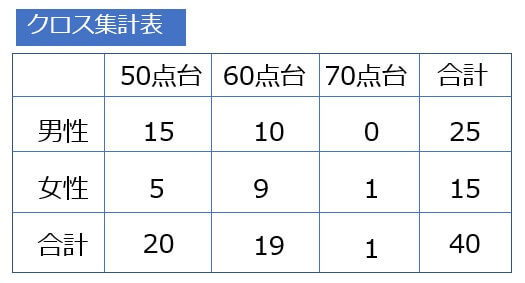
これをクロス集計表といいます(文字通り交差している表です)。
2変数に限らず3変数以上でもクロス集計表を利用することが出来ます。
観察度数と相対度数
これまでのように単純な度数で表すよりも、相対度数で表すほうが解析がしやすいです。
つまり相対的なパーセント表示にするわけです。
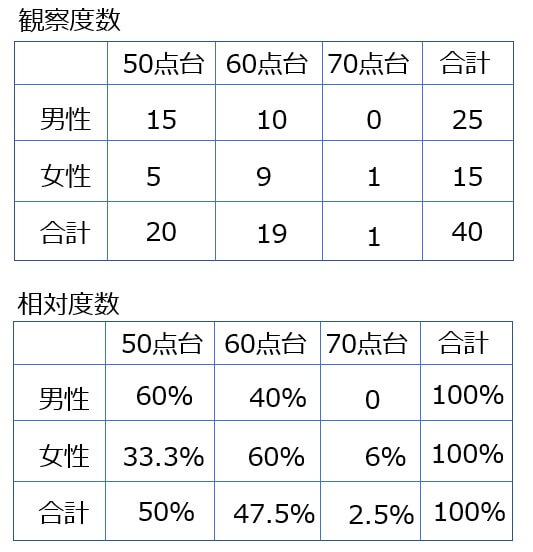
行パーセントと列パーセント
パーセント表示にするに当たって、行パーセントと列パーセントがありますね。
やってみればわかります。
行パーセントと列パーセントはそれぞれ意味が違いますから、違う情報が盛り込まれています。

相関係数
相関係数は変数間の関係を表すものですが、一般的に相関係数といえばピアソンの積率相関係数を指す場合が多いです。
ピアソンの積率相関係数は、2つの量的変数間の線形性を表し、-1~1の値で評価されます。
1であれば完全に正の相関、0なら相関なし、-1なら負の相関ということになります。
エクセルの活用
度数分布表とクロス集計表は、実際にエクセルで自分で作成してみると感触が得られると思います。
余裕のある方は以下の記事で作ってみてください。
エクセルのピボットテーブルを使えば簡単に作れます。
相関係数も数式を入力するだけで求められます。

過去問
第31回 問題88
量的データの集計や分析に関する次の記述のうち、正しいものを1つ選びなさい。
1 中央値とは、データの中で出現率が一番高い値のことである。
2 度数分布表は、一つの変数について、それぞれのカテゴリー(階級)に当てはまる度数をまとめたものである。
3 分散と標準偏差は、どちらも平均値からの分布度を示すが、これら二つの指標に関係はない。
4 クロス集計表により変数間の関係を考察するには、相対度数ではなく、観測度数を表示する。
5 ピアソンの積率相関係数は、二つの変数間の非線形関係を表している。
1 中央値とは、データの中で出現率が一番高い値のことである。
中央値は、順番に並べて真ん中にある値のことです。
最頻値と間違いやすいので注意です。
2 度数分布表は、一つの変数について、それぞれのカテゴリー(階級)に当てはまる度数をまとめたものである。
これが正解です。
3 分散と標準偏差は、どちらも平均値からの分布度を示すが、これら二つの指標に関係はない。
間違いです。
分散の平方根が標準偏差です。
4 クロス集計表により変数間の関係を考察するには、相対度数ではなく、観測度数を表示する。
逆です。
相対度数を用いるほうが変数間の関係を考察できます。
5 ピアソンの積率相関係数は、二つの変数間の非線形関係を表している。
非線形関係ではなく線形関係の強さを表す指標です。
第29回 問題88
量的調査におけるデータの集計方法に関する次の記述のうち、正しいものを1つ選びなさい。
1 クロス集計表において、セルの度数の比が全ての行で等しい場合、そのクロス集計表の2変数間には関連がない。
2 クロス集計表において、2変数間の関連をみる場合、行パーセント、列パーセントのどちらを示しても、得られる情報に変わりはない。
3 クロス集計表では、2変数間の関連を見ることができるが、3変数以上の関連についてはみることはできない。
4 度数分布表における相対度数とは、度数を合計した値を各カテゴリーの値で割って算出したものである。
5 連続変数では、値が連続的に変化するため、度数分布表を作成することができない。
1 クロス集計表において、セルの度数の比が全ての行で等しい場合、そのクロス集計表の2変数間には関連がない。
これが正解です。
2 クロス集計表において、2変数間の関連をみる場合、行パーセント、列パーセントのどちらを示しても、得られる情報に変わりはない。
間違いです。
得られる情報は違います。
3 クロス集計表では、2変数間の関連を見ることができるが、3変数以上の関連についてはみることはできない。
間違いです。
クロス集計表は3変数間でも関連を評価することが出来ます。
4 度数分布表における相対度数とは、度数を合計した値を各カテゴリーの値で割って算出したものである。
間違いです。
相対度数は、各カテゴリーの値を度数を合計した値で割った値です。
5 連続変数では、値が連続的に変化するため、度数分布表を作成することができない。
間隔尺度や比例尺度のデータである連続変数でも度数分布表を作成することができます。
例えば体重であれば、40kg台、50kg台、60kg台などと階級ごとにカテゴリー分けすれば度数分布表を作れます。
次の記事
次は、量的データの分析についてより広い内容を見ていきます。




コメント