度数分布表とクロス集計表の意味を理解するには自分で作ってみるのがベスト。
Excelで簡単に作れるので自分でやってみましょう。
テーブル作成
まずは、量的調査によって集計した以下のようなテーブルを作成します。
今回は、ある事業所の全利用者について、氏名、性別、身長、体重、障害支援区分をテーブルにしました。
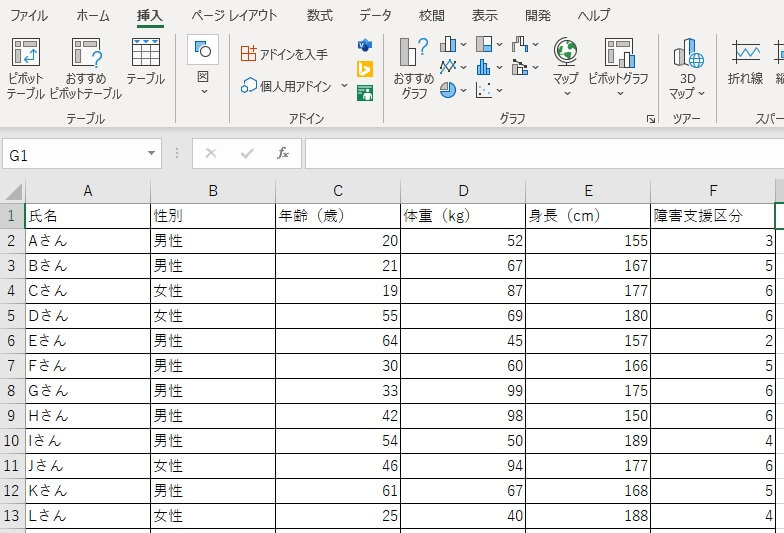
因みに、氏名、性別、年齢、身長、体重、障害支援区分はそれぞれ4種類のどの尺度かわかりますか?
以下の通りです。
障害支援区分は1~6までの6段階で支援の必要度を評価する指標でしたね。
6が最も手厚い支援が必要で、障害福祉サービスの中でも介護給付に属するサービスを受ける時は、障害支援区分認定を受けなければなりません。
障害支援区分は間隔には意味がありませんから間隔尺度ではなく順序尺度です。
順序尺度:障害支援区分
間隔尺度:
比例尺度:年齢、身長、体重
度数分布表(ヒストグラム)
それでは本題に入っていきます。
まずは、6段階の障害支援区分で、それぞれの区分の利用者が何人いるのか、集計しましょう。
「挿入」タブの左上に「ピボットテーブル」とあります。
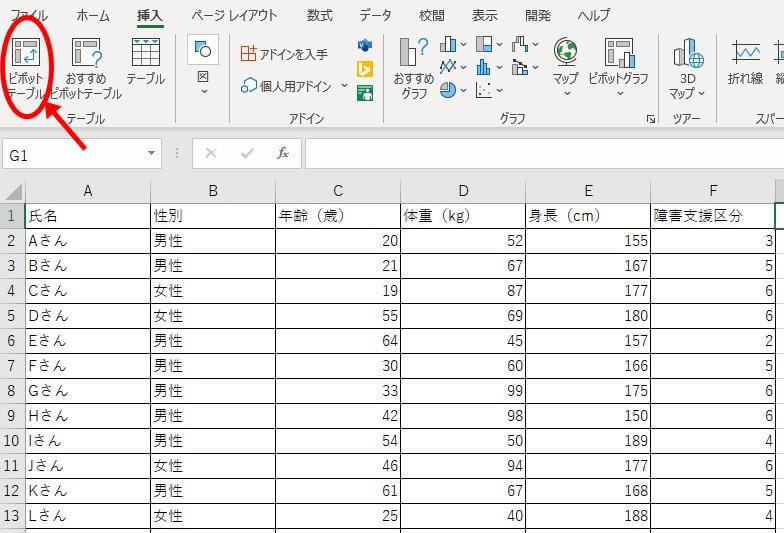
ピボットテーブルの右下「行」に注目したい「障害支援区分」を入れ、「値」には度数となる「氏名」を入れます。
するとピボットテーブルができました。
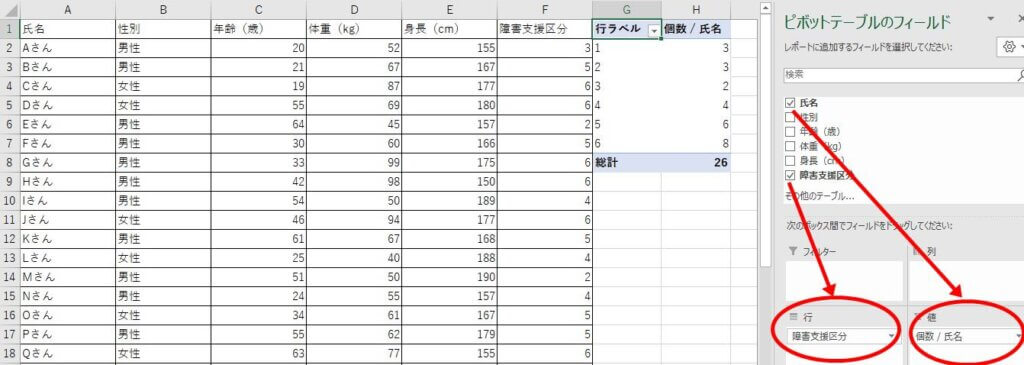
ピボットグラフを選択してグラフを作ると、度数分布表ができます。
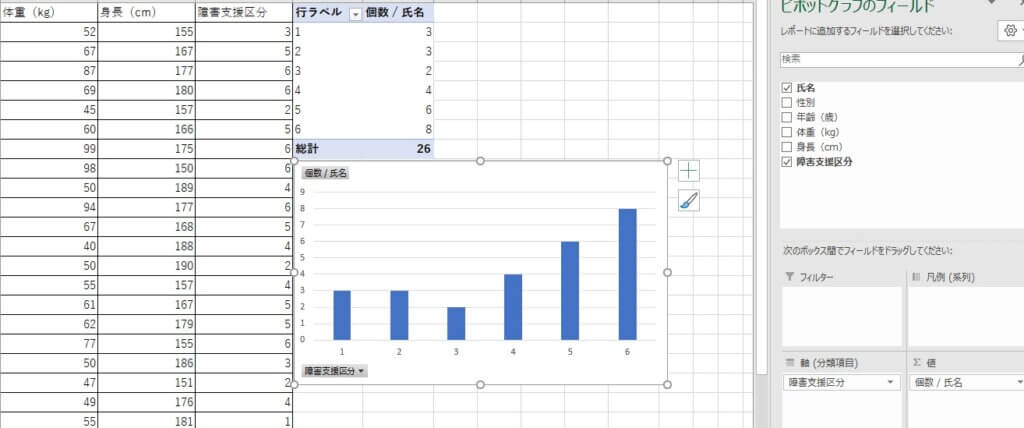
障害支援区分のそれぞれの値で、何人いるのか(度数)が棒グラフで表されています。
クロス集計表
クロス集計表は1変数だった度数分布表の2変数以上版です。
ピボットテーブルの右下、「列」のところに2変数目の項目を入れます。
今回であれば「体重」を入れます。
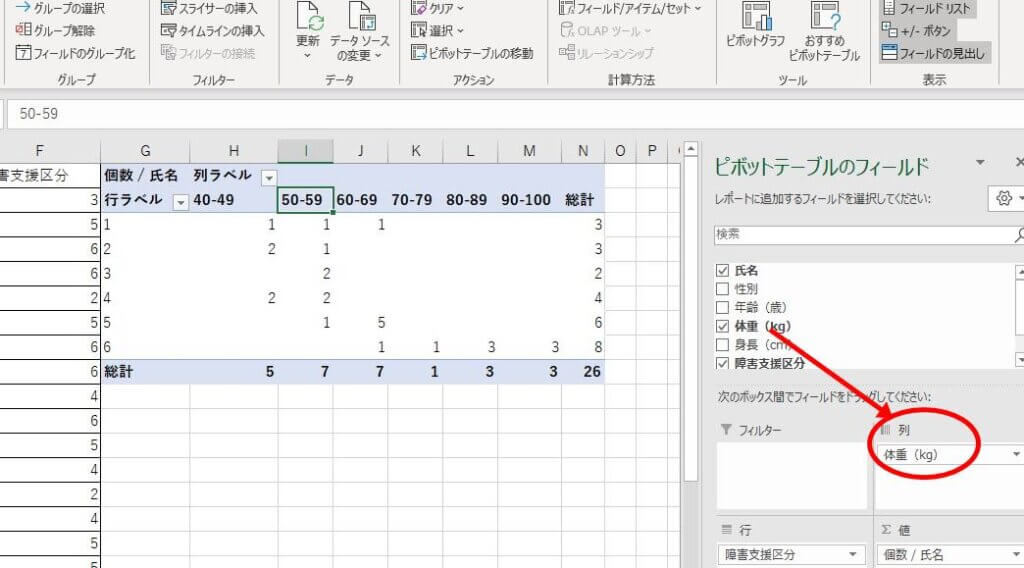
つまり、度数分布表というのは1つの変数についての度数を調べるのに対して、クロス集計表では2変数(以上)の度数を集計するので、2変数の相関が分かります。
クロス集計表をグラフにすると、以下のように3次元になります。
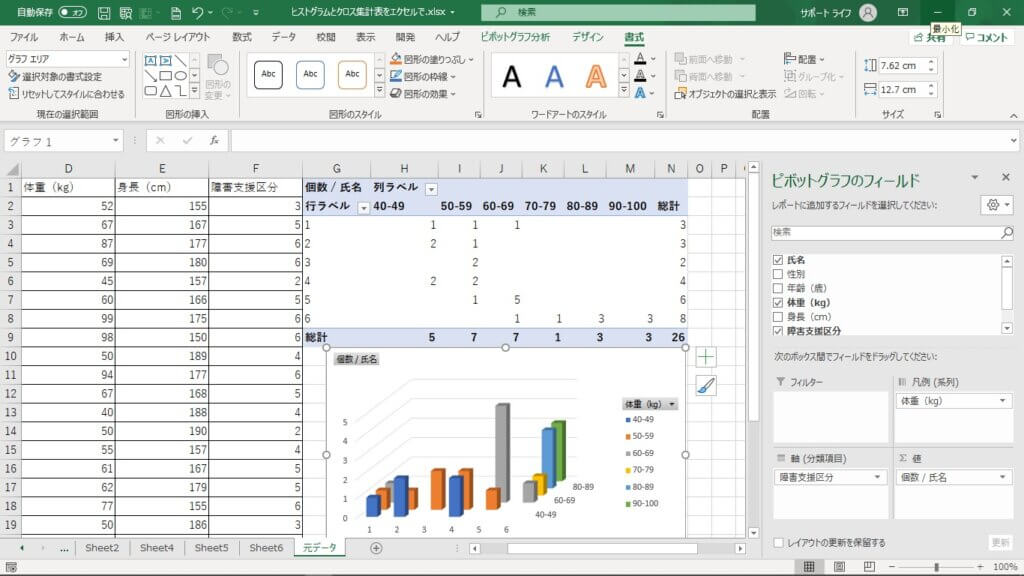
障害支援区分と体重という2変数についての人数(度数)が表されています。
では障害支援区分と体重には相関があるのでしょうか。
それを知るために、相関係数を求めます。
ピアソンの積率相関係数
相関係数にはいろいろあるのですが、2変数間の線形性を求める時にはピアソンの積率相関係数が用いられます。
ピアソンの積率相関係数は以下の数式で算出できます。
以下の例で見てみましょう。
体重と障害支援区分、身長と障害支援区分、それぞれで関係があるのか見てみます。
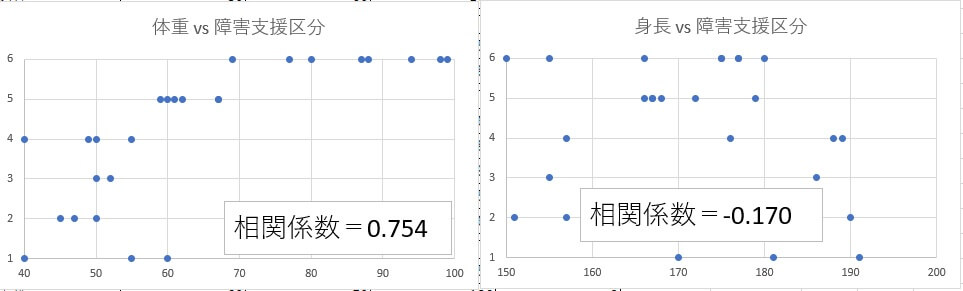
左のグラフは体重が増加すると障害支援区分も高くなっているように見えます。
右のグラフは身長と障害支援区分に相関はないように見えます。
左のグラフのような直線的な相関を線形性といい、ピアソンの積率相関係数は-1~1の値でその線形性を表します。
左は0.754で、「1」に近いほど線形です。
右のように「0」に近いと非線形で、「-1」に近づくと再び線形になります。
「1」は正の相関(右肩上がり)、「-1」は負の相関(右肩下がり)です。
過去問
第28回 問題87
ピアソンの積率相関係数に関する次の記述のうち、正しいものを1つ選びなさい。
1 値は0から1の範囲の間で変動する。
2 2つの変数の因果関係を表すものである。
3 年齢と所得の相関係数は、所得が円単位でもドル単位でも同じ値になる。
4 2つの変数の間に完全な相関がある場合、散布図は円形になる。
5 2つの順序変数の関連の強さを測る指標である。
1 値は0から1の範囲の間で変動する。
間違いです。
ピアソンの積率相関係数は「-1」~「1」の値を取ります。
ジニ係数は「0」~「1」の値を取るので混同しないよう。
2 2つの変数の因果関係を表すものである。
間違いです。
どちらが原因でどちらが結果かという因果関係は分かりません。
2変数の線形関係がわかるのみです。
3 年齢と所得の相関係数は、所得が円単位でもドル単位でも同じ値になる。
これが正解です。
4 2つの変数の間に完全な相関がある場合、散布図は円形になる。
間違いです。
完全な相関がある場合は、値は「1」か「-1」となり、直線になります。
5 2つの順序変数の関連の強さを測る指標である。
間違いです。
間隔尺度や比例尺度の関連の強さを測りますが、順序尺度を測るのには適していません。




コメント